(一)核心优化机制
The Little Learner
欢迎来到深度学习探索之旅！ 最近我系统学习了深度学习的原理，决定创作一个系列博客，与大家分享这段知识发现之旅。本系列将从最基础的概念起步，逐步深入到深度神经网络的原理与实践，最终目标是构建一个简易深度学习框架。无论您是零基础爱好者，还是想巩固根基的实践者，都能在此找到价值。
本系列内容主要源自《The Little Learner: A Straight Line to Deep Learning》——一本独具匠心的深度学习入门经典。在众多学习资料中选择它，源于其两大特色：苏格拉底式对话教学：通过问答形式逐步对每一个概念建立认知；函数式编程：采用Scheme语言。
虽然这种教学风格和语言并非主流，但正是这种独特性使其成为我的至爱。为了便于理解，在本文中我会尝试用大白话来代替对话体来对解释概念；并且以深度学习中占主导地位的编程语言Python替代Scheme。但是本系列文章的特色依然继承自原著：
- 简单，不假设读者有太多数学基础。读完本系列再去学习微积分、线性代数和概率论也会变得更容易；
- 函数式编程风格为主，虽然不使用Scheme,不过会保留函数式编程精髓。建议不熟悉的读者提前了解闭包、高阶函数等概念。
可能还是有人会问为何坚持函数式范式？首先当然是个人偏好；第二是函数式编程旨在尽量消除副作用，通过函数来传递数据等特点，使得数据流变得安全、清晰、容易思考。深度学习中通常包含大量数学表达式，大量传递数据，通常不包含太多有状态的组件，这些特点与函数式编程非常契合。这应该也是JAX,Pythorch等流行的库或者框架主要使用或者大量使用函数式编程范式的原因。
要想更好地理解本文，需要一些准备：
- Python基础：列表推导式、匿名函数和高阶函数等Python语法；
- 数学准备：仅需线性函数等基础概念，我们会探索所有必要知识；
- 开放的心态：本系列文章的行文和代码风格比较独特（对不熟悉的人来说）；一篇文章相当于书中三到四个章节，信息密度还是比较大的；加上本人难免会有疏忽大意的地方。需要读者在阅读的时候多多思考，自己尝试运行文中的代码、遇到bug自己debug……也欢迎联系我，提供你的反馈。
如果准备好了就开始吧。
简单线性函数
首先回忆一下中学学过的一次函数。表达式可能是：f(x) = wx + b或者y = kx + b。f(x)强调其函数性质；y表示一个值；系数用哪个字母表示没什么区别,在机器学习中常用w表示。w 来自英文单词 weight（权重），也被称为系数；b 来自 bias（偏移量）。
假设w = 1; b= 0在平面几何表示他们关系如下图：
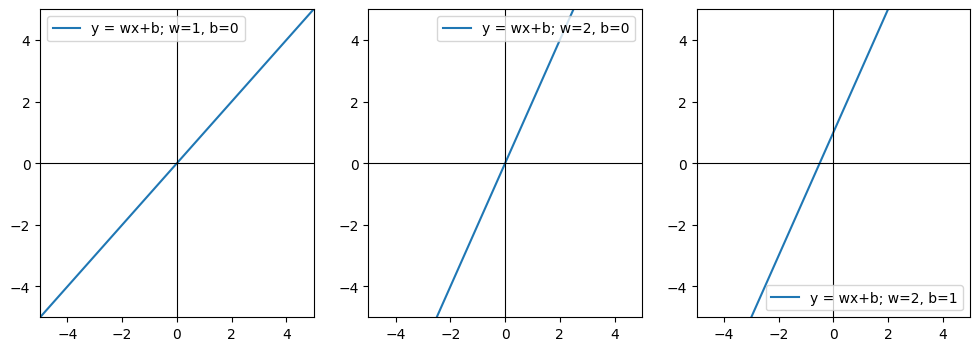
自变量x和因变量y的关系在平面直角坐标系中表示为一条直线时。这样的函数称为一次函数（linear function）。如果w的值改变y对于x的变化率会提升，如果b改变则会使整条直线会上下移动。
现在我们尝试用代码表示这个函数
from typing import Callable, Iterable, List
# 取值范围是实数；数据类型选择float.
def line(x: float) -> Callable[[float, float], float]:
return lambda w, b: w * x + b
这里line是一个高阶函数，当被调用时，它返回一个匿名函数。返回的函数需要w 和b两个参数，并从w和b得到最终结果，也就是因变量的值。
如果不熟悉高级函数而觉得难以理解的话，可以想象成一个函数接收x、w和b三个参数。之所以使用高级函数是因为之后处理自变量和系数以及偏移量的逻辑不相同。
看一个例子来帮助理解：假如知道w和b的值是1和0，想求x等于2的时候y的值。首先把2传给函数line，得到一个函数，再把1和0传给这个函数得到最终结果。
result = line(2)(1, 0) # result = 2
print(result) # 输出 2
问题
在数学课上可能更多地处理w和b已知，求自变量x的值的情况；然而，在机器学习中，我们通常面临的是另一种问题：已知一些x和y的值，需要根据它们学习(或估计)出 w 和 b 。
这里x就是自变量，也叫输入，在程序中是函数的参数；因变量y是x对应的输出值，也是函数的返回值。
x和y的值的集合在一起被称为数据集（dataset）；一个x和对应的y叫做一个数据点（data point）或样本（sample）；w和b被称为参数（parameter），一起被称为参数集（parameter set），常用希腊字母$θ (theta)$表示。在本文的例子中，$θ = [w, b]$。
现在假设有一组x的值 $[2.0, 1.0, 4.0, 3.0]$ 和对应的y值 $[1.8, 1.2, 4.2, 3.3]$，需要推导w和b。 可以画图表示这些数据点：
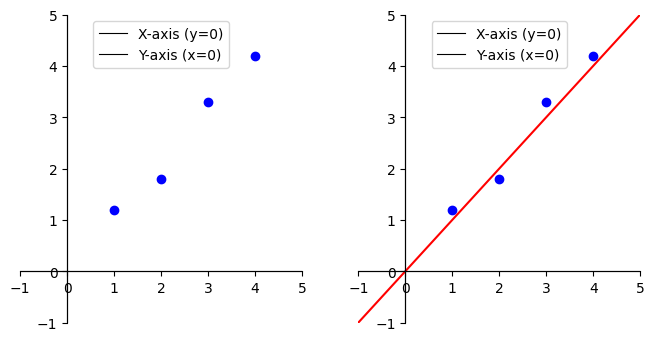
根据这几个点我们可以很容易想象出一条直线， 并且可以（通过肉眼）观察出w和b的值大概是多少。
看起来是个很简单的问题，不过怎么样能把这个过程写成程序然后让计算机解决这个问题呢？
思路
一个思路是使用 迭代优化(successive approximations) 的方法：先随机猜一组w和b的值，然后检查在该w和b值下，计算出来的y的值（我们称之为预测值y^）和正确的y之间的差距。然后不断调整w和b直到差距接近0。
如果我们随机选取 $θ = [0.0, 0.0]$ 即 $( w=0.0, b=0.0)$，对于数据点 $(x=2.0, y=1.8)$，预测的y值 line(2.0)(0.0, 0.0) 是 0.0。那么该参数下的预测值（通常表示为 ŷ, 读作 y-hat，就是给y带了一个帽子加以区分的意思）ŷ和y的差距是 $1.8 - 0 = 1.8$。这个数字也叫 损失（loss 或者 成本（cost） (在本文中，‘损失’和‘成本’指同一个概念——预测误差的总和，但在其他更严谨的资料中可能会用‘损失’指代单个样本，‘成本’指代整个数据集。)，它告诉我们当前的参数集$θ$距离“完美”拟合数据还有多大的改进空间。
把这个过程写成函数，就能很容易得到某个$θ$下某个x值的损失:
def loss_single(x: float, y: float, theta: list[float]) -> float:
pred_y = line(x)(*theta)
return y - pred_y
改进
这个初步的损失函数存在几个问题需要解决。
首先这个函数一次只处理一个值，我们希望它能对上面的数据集进行操作，因此需要改写line函数；其次，我们希望得到一个单一的数值来整体衡量误差大小，而非一个误差列表——列表无法直观地给出总体误差的度量。因此我们把所有的值加起来：
# 让line函数处理数组而不是单个数值
def line(xs: Iterable[float]) -> Callable[[float, float], List[float]]:
return lambda w, b: [w * x + b for x in xs]
# 需要先实现向量减法作为辅助函数，使得
# [a, b] - [c, d] = [a - c, b - d]……
def sub(ms: Iterable[float], ns: Iterable[float]) -> List[float]:
return [m - n for m, n in zip(ms, ns)]
def loss(xs: Iterable[float], ys: Iterable[float], theta: list[float]):
pred_ys = line(xs)(*theta)
errors = sub(ys, pred_ys)
return sum(errors)
虽然现在loss函数返回一个总值，但引入了一个新问题：如果一个预测偏高（差值为正），另一个预测偏低（差值为负），它们的损失加起来可能会相互抵消，使得总体损失看起来很小，但实际上每个点的预测都不准确。
为了解决这个问题，就需要消除列表中的负值。有两个方法可以做到：一个是取绝对值，一个是计算平方。两种方法得出来的结果分别叫做绝对损失（Absolute Loss）和平方损失（squared error），也叫做L1或者L2损失。两种方式各有其应该场景，对于回归任务，L2损失更合适，这里只实现L2损失。
对于单个数据点，L2损失可以这样计算：
#首先需要自定义square函数，让其可以用在可迭代数据上
def sqr(xs: Iterable[float]) -> List[float]:
return [x ** 2 for x in xs]
def l2_loss(xs: Iterable[float], ys: Iterable[float], theta: List[float]) -> float:
pred_ys = line(xs)(theta)
errors = sub(ys, pred_ys)
sqr_err = sqr(errors)
loss = sum(sqr_err)
return loss
我们的目标是找到一个$θ$，使得整个数据集上所有数据点的L2损失之和最小。也就是说我们需要套用损失函数，求出误差值作为参考不断迭代$θ$。在这个过程中l2_loss函数是我们优化的目标，也把它被称为目标函数（objective function），有时候会用英文字母$J$表示。
我们不希望在每次更新$θ$时都重复传入整个数据集；而且这个函数的内部调用了line函数，这意味着当前的l2_loss函数与line模型强耦合；我们希望构建一个通用的损失函数，能够适配不同的模型。这两个问题可以通过把该函数改写成高阶函数来解决——把line函数, xs, ys作为外层函数的参数，将模型函数和目标数据固定下来（这种方式称为闭包（closure）），生成一个只依赖于θ的损失函数：
def l2_loss(target: Callable[[Iterable[float]], Callable[[float, float], List[float]]]) -> Callable:
def expectant(xs: Iterable[float], ys: Iterable[float]) -> Callable:
def objective(theta: list[float]) -> float:
pred_ys = target(xs)(*theta)
errors = sub(ys, pred_ys)
return sum(sqr(errors))
return objective
return expectant
现在可以把数据带入进去测试一下了：
# 数据集
line_xs = [2.0, 1.0, 4.0, 3.0]
line_ys = [1.8, 1.2, 4.2, 3.3]
# 初始猜测 θ
initial_theta = [0.0, 0.0]
# 计算初始损失
line_objective = l2_loss(line)(line_xs, line_ys)
current_loss = line_objective(initial_theta)
print(f"使用 θ = {initial_theta} 时，总L2损失为: {current_loss}")
# 输出大约是 33.21 (1.8^2 + 1.2^2 + 4.2^2 + 3.3^2)
迭代
写一个函数来帮助完成迭代过程：
def revise(revision_func: Callable[[list[float]], List[float]],
num_revisions: int,
initial_theta: List[float]) -> List[float]:
current_theta = initial_theta
for _ in range(num_revisions):
# 也可以保留更新历史用于可视化
current_theta = revision_func(current_theta)
return current_theta
这个函数有三个参数：第一个是迭代函数或者叫做优化算法它告诉我们如何迭代$θ$的值；第二个是迭代次数；第三个是初始化的$θ$值。
接下来需要一个迭代算法。比如每次让w的值比之前增加0.01，迭代200次，看看l2_loss返回值的变化：
def update_v0(theta: List[float]) -> List[float]:
w, b = theta
w += 0.01
return [w, b]
为了观察损失值随参数$θ$的变化情况，我们需要记录每次更新后的$θ$值及其对应的损失：
training_history = revise(update_v0, 200, initial_theta)
ws = [theta[0] for theta in training_history]
losses = [objective(theta) for theta in training_history]
绘制w和loss的关系图得到：
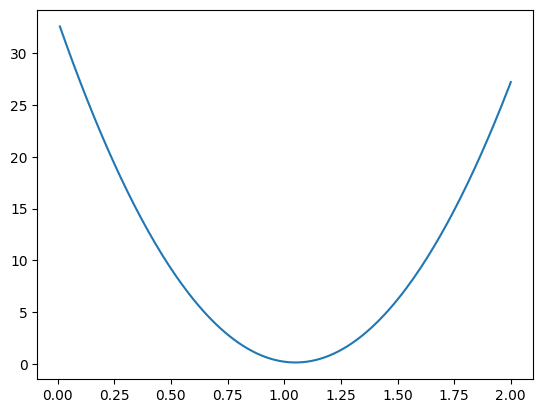
现在可以看图目测得到一个合理的$θ$值……显然，update_v0是一个非常朴素的算法，它无法智能地判断何时接近最优解，也无法保证损失值持续下降。我们需要一种更智能的方法，能够引导损失值稳定地朝向最小值（理想情况下是$0$）下降，这将会是下一篇文章的主题。
总结
在文章的最后，让我们回顾一下本文的核心内容。本文其实只讲了一个核心主题——优化机制(Optimization Mechanism），也就是如何调整模型参数以最小化或最大化目标函数的过程。它是机器学习的数学引擎，贯穿模型训练的始终。
本文是从最简单的线性函数出发，在本系列后面的文章中会看见更复杂的线性函数，非线性函数以及神经网络等复杂模型；L2损失函数，作为目标函数，是本文的重点内容，希望读者能掌握。之后也会了解其他类型的目标函数；本文还未涉及到合理的优化算法，下一篇文章将会介绍深度学习中最核心的优化算法——梯度下降，敬请期待。