(二)梯度下降

回顾与展望

欢迎来到零基础深度学习系列的第二篇内容。

本文的内容紧接上一篇遗留的问题——在上一篇文章中，我们定义了最基础的线性模型，目标函数以及用于参数更新的辅助函数，但尚未实现有效的优化算法。

本文将从目标函数曲线切入，逐步介绍机器学习最核心的优化算法——梯度下降法。有了有效的优化算法，便可以让计算机自己完成整个学习过程。为测试算法通用性，我们将引入的更多模型，并可能发现值得探索的新问题。

本文延续使用上篇定义的line、l2_loss和revise等函数，理解这些函数的作用和内部结构是掌握本文以及后续内容的基础，因此如果你还没有读过本系列上一篇文章的话，建议优先阅读。

梯度的数学意义与计算

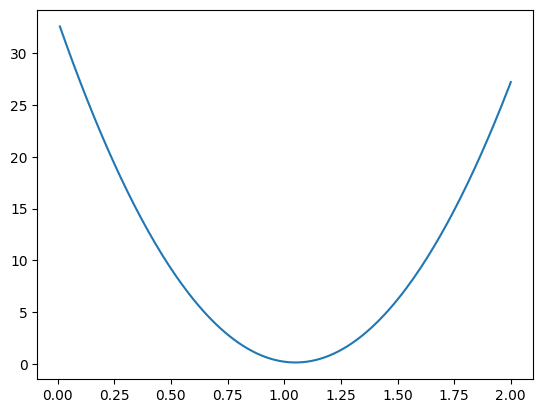
上一篇文章最后，我们可视化了目标函数值随参数w的变化趋势： w-loss

该图揭示关键现象：目标函数值并非随参数线性变化，而是呈现非线性曲线关系。这表明目标函数的变化速率是动态的，解释了为何固定步长（如每次增加0.01）的优化方式效率低下且缺乏智能性。

由此引出一个洞见：通过计算目标函数对参数的瞬时变化率，可以动态调整参数更新方向与幅度：即变化率较大时，表明离最优解较远，可增大步长；变化率较小时，可能接近最优解，需减小步长以防震荡

让我们用具体数值理解这个概念：

假设当前$θ=[0.0, 0.0]$，目标函数值为33.21。当我们将w微增到0.0099时，目标函数值变为32.59。变化量计算如下：

\[\text{变化量} = (32.59 - 33.21) = -0.62\] \[\text{瞬时变化率} = \text{变化量} / \text{微增量} = -0.62 / 0.0099 ≈ -62.63\]

该值($-62.63$)即目标函数在当前点的瞬时变化率（曲线的斜率），几何上表示为曲线在该点的切线。整个参数集（如w、b）对目标函数的瞬时变化率（一个向量）叫做梯度(gradient) ，表示该参数集对目标函数的综合影响。

若熟悉微积分，可看出求梯度即计算参数集的偏导数(partial derivative)。求梯度运算常用$\nabla$表示，该符号读作”nabla”，该运算又称为del算子（两种读法皆可）。

接下来我们尝试写程序来让计算机帮助完成这个操作：

# 函数名叫做nabla，因为del是python里的关键字

def nabla_single(objective_func: Callable[[List[float]], float],
          p: float,
          delta: float = 1e-6) -> float:

    current_loss = objective_func(theta)
    perturbed_theta = p + delta
    perturbed_loss = objective_func(perturbed_theta)
    gradient = (perturbed_loss - current_loss) / delta
    return gradient

参数delta参数代表微增量，是一个非常小的数值，也可以自定义，比如使用上面的0.0099。

不过这个函数只能处理单个参数的情况，而我们需要一个更通用的梯度计算函数，能够接受任意数量的参数。

def nabla(objective_func: Callable[[List[float]], float], 
          theta: List[float], 
          delta: float = 1e-6) -> List[float]:
    
    current_loss = objective_func(theta)
    
    def get_grad(theta: List[float], i: int) -> float:

        theta[i] += delta
        new_loss = objective_func(theta)
        return (new_loss - current_loss) / delta

    gradients = [get_grad(theta.copy(), i) for i in range(len(theta))]
    return gradients

这个函数看起来复杂了一些，但是其实先把计算导数的逻辑抽象出来，然后用列表推导式遍历参数而已。有了计算梯度的方法，接下来我们利用梯度信息来更新参数。

学习率：优化步伐的调节器

梯度包含两个关键信息：

方向（符号）：负梯度指示目标函数下降方向
强度（绝对值）：值越大表示优化空间越大

但是具体做出多大的调整（确定具体步长）依然是一个问题。

假如我们直接按照梯度大小来调整：

# 初始参数
theta = [0.0, 0.0]

# 计算梯度
grad = nabla(objective_func, theta)  # 假设返回[-62.63, -12.4]

# 直接使用梯度更新
new_theta = [theta[0] - grad[0], theta[1] - grad[1]]  # [62.63, 12.4]

# 得出损失
print(line_objective(new_theta))

这个参数的出来的损失高达$113,763.027$！这就像从山坡上跳向谷底，结果飞过了整个山谷，并且冲上了天空。

为了解决这个问题，我们用一个小常数(通常$0.001-0.1$)乘以梯度，来控制更新步伐。这个小的常数叫做学习率(Learning Rate)，用希腊字母$\alpha$表示。

下面的例子中会让学习率等于0.01。引入变化率会使每次参数的更新量很小，但是确保了损失在稳步下降。

学习率本身不是模型参数，但对参数优化过程至关重要。此类不通过数据学习而需人工设定的配置的变量被称为超参数(hyperparameter)。其实此前我们已接触过另一个超参数——revise函数中的迭代次数。

你可能想知道怎么确定超参数，目前为止只是凭借经验，后面会提到一种叫做网格搜索的超参数优化方法，敬请期待。

接下来看一眼参数更新公式的数学表示：

\[\theta_{\text{new}} = \theta_{\text{old}} - \alpha \cdot \nabla J(\theta_{\text{old}})\]

其中：α是学习率 $\nabla J(\theta)$ 是目标函数在$θ$处的梯度。这里每一个字母的含义都已经做过介绍，应该是非常好理解的。

迭代更新函数：

learning_rate = 0.01

def update_v1(theta: List[float]) -> List[float]:
  
    # 求导
    grad = nabla(line_objective, theta)
    # 根据导数g和学习率learning_rate更新参数
    # 这里假设了p和g都是数值，可以直接应用乘法和减法
    return [p - learning_rate * g for p, g in zip(theta, grad)]

测试一下这个更新函数好不好用：

theta_history = revise(update_with_loss(update_v1), 1000, initial_theta)

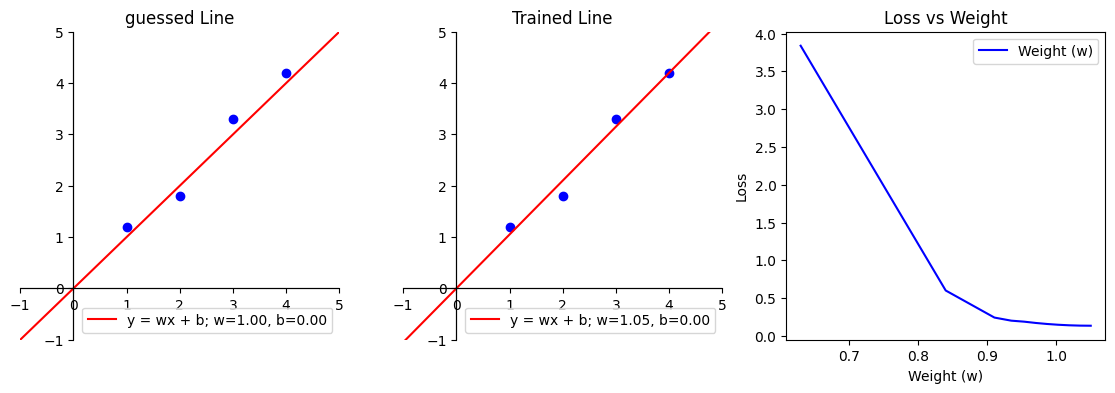
得到的结果是[1.0499806157842302, 6.016510481423397e-05]这跟我们之前预测非常接近，画图来看几乎看不出区别。从目标函数值的变化率也可以看出来，损失在逐渐接近0。 trained line

实现梯度下降

接下来，我们将上述辅助函数整合为统一的梯度下降接口。该接口应该设计为通用接口，可应用于任意模型（不限于线性模型）。我们把目标函数，初始参数和学习率等设置为参数。

def gradient_descent(objective_func: Callable[[List[float]], float],
                     initial_theta: List[float],
                     learning_rate: float,
                     num_revisions: int) -> List[float]:

    # 与update_v1相同
    def update(theta: List[float]) -> List[float]:
        
        grad = nabla(objective_func, theta)
        
        revised_theta = [p - learning_rate * g for p, g in zip(theta, grad)]
        return revised_theta

    return revise(update, num_revisions, initial_theta)

首先复制之前的update_v1……不过它在gradient_descent函数内部，这意味这它是一个闭包结构：它访问函数内部的目标函数，而不是全局作用域的。最后调用revise函数来更新参数。

为验证梯度下降的泛化能力，我们尝试二次函数拟合任务。

它的数学表达式是：$ y=ax^2+bx+c $。

python代码：

# 首先定义函数
def quadratic(xs: Iterable[float]) -> Callable[[float, float, float], List[float]]:

    return lambda a, b, c: [a * x**2 + b * x + c for x in xs]

quad_xs = [-1.0, 0.0, 1.0, 2.0, 3.0]
quad_ys = [2.55, 2.1, 4.35, 10.2, 18.25]

# 初始参数全部设置为0
initial_quad_theta = [0.0, 0.0, 0.0]

# 目标函数
quad_objective = l2_loss(quadratic)(quad_xs, quad_ys)

# 运行梯度下降
optimized_quad_theta = gradient_descent(
    objective_func=quad_objective,
    initial_theta=initial_quad_theta,
    learning_rate=0.001,  
    num_revisions=1000   
)[-1]

print(f"二次函数参数: a={optimized_quad_theta[0]:.4f}, b={optimized_quad_theta[1]:.4f}, c={optimized_quad_theta[2]:.4f}")

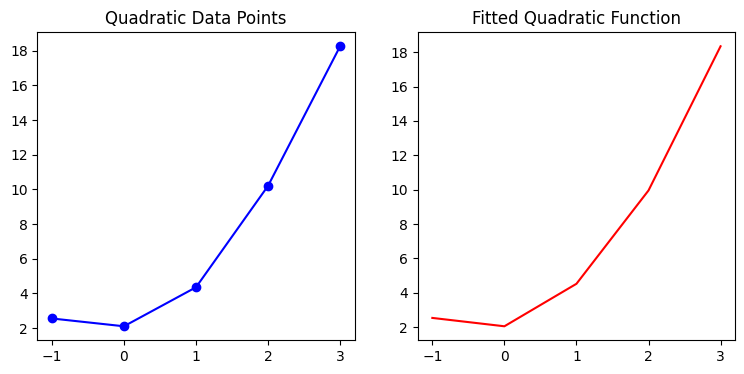
输出示例：二次函数参数: 二次函数参数: a=1.4787, b=0.9929, c=2.0546 可是化数据和训练结果：二次函数训练结果

看来该梯度下降实现能有效处理非线性问题。我们进一步尝试高维线性模型（平面拟合）：$y = w_1x_1 + w_2x_2 + … + w_nx_n + b$。

此时权重$w$扩展为向量。

#为了便于后续操作，先实现点积函数，也就是两个列表中的对应值相乘，然后求出乘积的和：
def dot_product(v1: Iterable[float], v2: Iterable[float]) -> float:

    return sum(x * y for x, y in zip(v1, v2))


def plane(xs: Iterable[Iterable[float]]) -> Callable[[Iterable[float], float], List[float]]:

    return lambda w_vector, b: [dot_product(x, w_vector) + b for x in xs]

# 新的数据集
plane_xs = [(1.0, 2.0), (2.0, 3.0), (3.0, 4.0), (4.0, 5.0)]
plane_ys = [1.0 * x[0] + 0. 5 * x[1] + 0.1 for x in plane_xs]

# 初始参数 (w1, w2, b)
initial_plane_theta = [[0.0, 0.0], 0.0]


# 目标函数
plane_objective = l2_loss(plane)(plane_xs, plane_ys)

# 运行梯度下降
optimized_plane_theta = gradient_descent(
    objective_func=plane_objective,
    initial_theta=initial_plane_theta,
    learning_rate=0.001,
    num_revisions=5000
)
# TypeError: 'float' object is not iterable

运行后出现类型错误。原因在于：当前nabla和update函数都假设参数是平展列表(flat list)，也就是列表的元素都是浮点数，但高维模型中的参数可能是嵌套结构（比如这里每一个输入和每一个权重也是一个数组结构）。这暴露了当前实现的维度局限性。

修改nabla和update函数能让测试通过，可以自行尝试。要想比较优雅地解决这个问题，还需要先学习一个概念，我们下一篇文章处理。

有趣的是，书中这个测试也通过了。原因是书中更早的时候就介绍了更复杂和数据结构以及操作；而且并没有给出nabla函数——也就是数值微分——的实现方案，想尝试书中代码的时候也只需要调用库函数。这么设计的原因是想专注于理解神经网络的相关概念。对微积分比较了解的朋友可以想一想怎么用链式法则来完成自动求导。

总结

在本文中，我们深入探索了梯度下降算法。其核心在于：

梯度计算 - 确定优化方向

学习率控制 - 调整优化步长

迭代更新 - 逐步逼近最优解

通用性验证：成功应用于线性、二次函数的拟合。

恭喜，读完本文你已经了解了整个训练线性模型/学习参数的过程。不过当前实现是梯度下降的基础版本，后续将探索更多变体和优化方案。况且你可能还不知道这跟神经网络或者深度学习到底有什么关系。

当前急需解决的问题是基于列表实现的函数无法处理高维数组。虽然可以暂时修改函数的实现逻辑来临时解决问题，但是更好的办法是寻找一个通用的解决方案，而这正是下一篇文章的主题。我们将会从一个非常酷的概念——张量（tensor）入手，到彻底解决所有高维数组操作问题。

现在先休息一下吧。