(四) 优化器

引言：优化器的重要性

欢迎回到深度学习探索之旅！在前三篇文章中，我们建立了线性模型基础（一）、实现了梯度下降算法（二）、并引入了张量数据结构（三）。不过面对真实场景中的海量数据与高维模型，传统批量梯度下降在速度与收敛稳定性（更平稳地找到最低点）上的瓶颈日益凸显。于是，研究者提出了一系列改进策略，这些策略被统一封装为优化器（optimizer），让训练更快、更稳，也更容易使用。

本文将带您深入探索梯度下降的进化之路，从最基础的批量梯度下降出发，逐步揭示四大里程碑式优化器：

随机梯度下降（SGD） - 大数据时代的敲门砖
动量法（Momentum） - 物理学启发的加速器
RMSProp - 自适应学习率
Adam - 集大成者

随机梯度下降：大数据的解决方案

批量计算的困境

在之前的实现中，我们每次迭代都使用整个数据集计算梯度：

plane_objective = l2_loss(plane)(plane_xs, plane_ys) # 目标函数
gradient = nabla(objective_func, theta)  # 计算梯度

目标函数是闭包，可以访问整个数据集。当数据集非常大的时候，单次梯度计算可能非常耗时！这就如同一个果农不确定苹果是否成熟了，结果把每个苹果都尝了一遍才能得出结论。

随机抽样的智慧

当然，果农只会随机品尝几个苹果，然后用这几个苹果的味道来近似评估整箱的品质。虽然单次评估可能存在偏差，但多次随机品尝后，我们同样能对整箱苹果的品质有一个相当准确的了解，而且速度快得多。

把这个原理运用到梯度下降中，也就是说不用每次都使用所有的数据，而是使用一部分随机样本：

# 引入random模块用于随机采样
import random

def sampling_obj(
    full_objective: Callable,  # 完整数据集的目标函数
    xs: Tensor,                # 全部输入数据
    ys: Tensor,                # 全部标签数据
    batch_size: int = 32       # 批次大小（超参数）
) -> Callable:
    """创建基于小批次的目标函数"""
    n = len(xs)
    
    def minibatch_objective(theta: Theta):
        # 随机选择批次索引
        batch_indices: list[int] = random.sample(range(n), batch_size)
        
        # 构建小批次数据
        xs_batch = [xs[i] for i in batch_indices]
        ys_batch = [ys[i] for i in batch_indices]
        
        # 创建批次目标函数
        batch_objective = full_objective(xs_batch, ys_batch)
        
        return batch_objective(theta)
    
    return minibatch_objective

# 引用
plane_simple_objective = sampling_obj(l2_loss(plane), plane_xs, plane_ys, 4)

以后训练的时候可以使用这个函数代替l2_loss作为目标函数。它的原理依然使用闭包记住所有数据，但是每次训练的时候只提供随机选中的部分给真正的目标函数，也就是l2_loss（我们目前只学了这一个目标函数）。

使用这个目标函数的梯度下降就是随机梯度下降（Stochastic Gradient Descent）。

SGD的价值

使用SGD以后，计算复杂度从O(N)降到O(B)，其中B是批次大小，N是实际训练数据量。SGD也引入梯度噪声，不过适度噪声反而有助于逃离局部极小值。

批次大小batch_size这个超参数的选择需要权衡利弊：批次小则迭代快，噪声多；批次大则梯度准，内存消耗高。

模块化梯度下降

在学习更多的优化器之前，需要先重构一下梯度下降。

在之前的实现中，梯度下降是一个入口函数，它包裹着一个更新函数，然后调用一个循环函数来完成参数的多次更新。不同的梯度下降优化器主要区别是更新函数的区别，换句话说我们可以通过修改更新函数来轻松实现不同变体的梯度下降算法。

具体来说，更新函数负责处理参数的更新逻辑。如果我们对梯度下降的变体进行抽象，可以发现更新函数的输入和输出并不仅限于参数集本身，还可以包含其他辅助信息。为了实现这一点，我们需要两个额外的函数：一个用于包装参数，另一个用于解包装。

来看代码：

# 超参数越来越多了，所以用一个容器来承载它们
class GDConfig:
    """梯度下降超参数容器
    Attributes:
        lr: 学习率 (默认0.01)
        revs: 迭代次数 (默认200)
        batch_size: 批次大小 (默认4)
    """
    lr: float = 0.01
    revs: int = 200
    batch_size: int = 4

def gradient_descent_builder(
    inflate,   # 参数包装函数 (普通参数 → 优化器专用结构)
    deflate,   # 参数解包函数 (优化器结构 → 普通参数)
    update     # 参数更新逻辑 (实现优化算法核心)
):
    """
    优化器工厂函数
    返回一个配置完备的优化器
    """
    def optimizer(objective: Callable, initial_theta: Theta, hyper: GDConfig):

        # 对初始参数进行包装
        initial_inflated_theta = [inflate(param) for param in initial_theta]

        # 定义一个修订步骤函数，用于在每次迭代中更新参数
        def revision_step(inflated_theta: Any):

            # 对包装后的参数进行解包装
            theta = [deflate(P) for P in inflated_theta]

            # 计算梯度
            gradients = nabla(objective, theta, delta=1e-6)

            # 使用更新函数来更新包装后的参数
            next_inflated_theta = [
                update(p, g, hyper) for p, g in zip(inflated_theta, gradients)
            ]

            # 返回更新后的包装参数
            return next_inflated_theta

        # 调用修订函数进行多次迭代更新
        training_history = revise(revision_step, hyper.revs, initial_inflated_theta)

        # 对训练历史中的参数进行解包装并返回
        return [[deflate(p) for p in i_theta] for i_theta in training_history]

    # 返回一个根据给定的包装、解包装和更新函数构建的优化器函数
    return optimizer

gradient_descent_builder函数返回的函数optimizer 和gradient_descent函数是一样的；不过update函数变成了revision_step。现在update函数只实现更新参数更新规则，其余的部分，比如求梯度，保留在revision_step函数中。

注意上一篇说过每一个参数都是一个张量，但是参数集本身不是张量，所以把每个参数和对应的梯度分别传递给更新函数。

重新实现基础梯度下降:

# 恒等包装/解包
def naked_i(p: P) -> P: return p
def naked_d(p: P) -> P: return p

# 基础更新规则: θ = θ - α·∇J
def naked_u(p: Tensor, g: Tensor, hyper: GDConfig):
    return tsub(p, tmul(g, hyper.lr))

# 构建基础优化器
naked_gd = gradient_descent_builder(named_i, named_d, named_u)

动量 (Momentum)

想象四个兄弟跑接力。老大跑风一样快，老二老三一个比一个慢，老四慢得离谱。聪明的教练让每个人在交棒时都先不松手——跑得快的人拽着慢的一起冲，把速度一点点传过去。结果全队整体时间大幅缩短。

因为这个过程和物理学中的动量/势能概念相似，所以使用动量法作为这个优化器的名字。动量法通过引入一个“速度”（velocity）向量来实现这一点，该向量是过去梯度更新的累积。

具体来说，参数更新不再只依赖当前的梯度，而是当前梯度与前一步“速度”的结合。这种结合通过一个动量系数来控制，动量系数通常是一个接近1的值（例如0.9）。

动量代码实现

下面是动量法的实现：

from collections import namedtuple

VelocityP = namedtuple("VelocityP", ["parameter", "velocity"])

@dataclass(frozen=True)
class MGDConfig(GDConfig):
    momentum: float = 0.9  # 动量系数，常用希腊μ或者β1表示

def velocity_i(p: P) -> VelocityP:
    """参数初始化：附加零速度向量"""
    return VelocityP(p, zeros(p))

def velocity_d(vp: VelocityP) -> P:
    """解包：提取原始参数"""
    return vp.parameter

def velocity_u(vp: VelocityP, g: Tensor, h: MGDConfig) -> VelocityP:
    """动量更新规则：
    1. 更新速度: v = μ·v_old - α·∇J
    2. 更新参数: θ = θ + v
    """
    v = tsub(tmul(h.momentum, vp.velocity), tmul(h.lr, g))
    p = tadd(vp.parameter, v)
    return VelocityP(p, v)

# 构建动量优化器
mgd = gradient_descent_builder(velocity_i, velocity_d, velocity_u)

动量公式解释

如果你没有看明白动量更新规则，使用一点简单的加法交换律和结合率会让事情变得更容易：

$v = μ \cdot v_\text{old} - \alpha \cdot \nabla J(\theta_{\text{old}})$ $\theta_{\text{new}} = \theta_{\text{old}} + v$ $\theta_{\text{new}} = \theta_{\text{old}} - \alpha \cdot \nabla J(\theta_{\text{old}}) + μ \cdot v_\text{old}$

最后这个公式的前一部分就是我们已经非常熟悉的梯度下降更新公式，后面加上了$ μ \cdot v_\text{old}$。在这个公式中$ v_\text{old}$代表的是历史累计的梯度，只要方向一致，它就会越来越大，像雪球滚下山；一旦方向反了，它就会慢慢刹车甚至掉头。其中$\mu$在代码中是momentum的常数变量，这个超参数决定了$v_\text{old}$历史梯度或者Velocity的权重或者说占比。$\beta = 0$的时候就变成了传统的SGD或者基础版的梯度下降；μ 越接近 1，雪球越重，下坡越快。

其实这是一个简化版的动量更新公式，还有另一个动量公式： $v_\text{t} =μ v_\text{t−1} +(1−μ )\alpha∇ J(θ) 2$ 通过这个公式更能清晰地看出超参数$\mu$的作用。这两个公式是等价的，区别仅在于是否将学习率$\alpha$包含在动量项中。这种方法省一次乘法，在代码实现中更常见。

动量效果解析

通过引入动量，我们在更新参数时不仅考虑了当前的梯度，还结合了之前的速度。这使得算法在正确的方向上能够加速，并在遇到震荡时能够平滑过渡。在一些情况下，这种加速效果可以显著减少训练所需的迭代次数。

例如，在我们的例子中原本可能需要训练5000次才能达到的结果，使用动量法后可能只需要训练500次。这种加速效果在处理大型数据集时尤其明显。

动量法的特点还可以从可视化参数变化看出来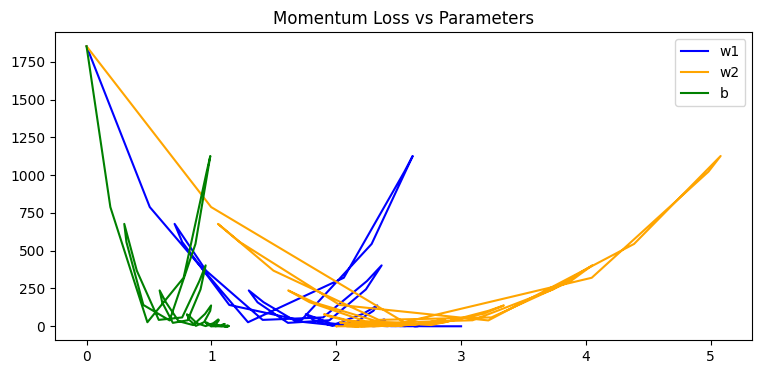因为动能的加持，速度过快会冲过头，或者在底部震荡，这个特点也有助于冲过局部低点。

RMSProp: 自适应学习率

无论是标准梯度下降还是动量法，我们都对所有参数使用了同一个学习率learning_rate。但有时，不同的参数可能需要不同的更新步长。例如，某个参数的梯度一直很大，我们可能希望减小它的学习率以防更新过头；而另一个参数的梯度很小，我们则希望增大学习率让它更新得快一些。

RMSProp (Root Mean Square Propagation) 算法就实现了这种自适应学习率。它为每个参数维护一个该参数梯度平方的移动平均值。在更新参数时，学习率会被这个移动平均值的平方根所除。

RMSProp实现

先看代码：

@dataclass(frozen=True)
class RMSPropConfig(GDConfig):
    decay: float = 0.9    # 梯度平方衰减率常用α或β2表示
    eps: float = 1e-8     # 数值稳定常数

# 定义参数结构：存储参数+梯度平方移动平均
RmsP = namedtuple("RmsP", ["parameter", "running_avg"])

def rms_i(p: P) -> RmsP:
    """初始化：附加零值移动平均"""
    return RmsP(p, zeros(p))

def rms_d(rms_p: RmsP) -> P:
    """解包：提取原始参数"""
    return rms_p.parameter

def smooth(decay: float, average: Tensor, g: Tensor) -> Tensor:
    """计算指数移动平均：new_avg = β·old_avg + (1-β)·g²"""
    return tadd(tmul(decay, average), tmul(1 - decay, g))

def rms_u(rms_p: RmsP, g: Tensor, h: RMSPropConfig) -> RmsP:
    """RMSProp更新规则：
    1. 更新移动平均: r = β·r_old + (1-β)·(g⊙g)
    2. 计算自适应学习率: lr_eff = α / (√r)+ ε
    3. 更新参数: θ = θ - lr_eff·g
    """
    r = smooth(h.decay, rms_p.running_avg, tsqr(g))
    new_lr = tdiv(h.lr, tadd(tsqrt(r), h.eps))
    p = tsub(rms_p.parameter, tmul(new_lr, g))
    return RmsP(p, r)

理解RMSProp公式

RMSProp的更新规则分为两步：

\[r_\text{t} =βr_\text{t−1}+(1−β)∇θJ(θ)^2\] \[θ_\text{t}=θ_\text{t−1}−\frac{α}{\sqrt{r_\text{t}}+ϵ} ∇J(θ)v t\]

要理解这两个公式还是先从我们熟悉的梯度更新入手。首先我们需要动态的学习率，这点很容易——只需要给学习率乘以一个变量就好了；然后我们需要这个变量在梯度值大的时候它的值比较小，在梯度小的时候，它的值比较大，这点用倒数实现，这个变量值越大，它的倒数值就越小；这也引出一个问题，这个变量的值可能为0，分数分母如果等于0，则表达式无意义，因此加上一个很小的常数ϵ以避免除零错误。以上就是公式中的$\frac{α}{\sqrt{r_\text{t}+ϵ}}$的由来。这个公式作为新的学习率，在代码中体现为newlr变量。

接下来是$\sqrt{r}$的来历：它的值应该反映梯度的大小，但是不能直接使用梯度，因为$\frac{\alpha}{g} \cdot g = \alpha$，这样的话就等于失去了梯度信息。所以我们用和上文中求动量中几乎一样的方法(smooth函数)求出梯度平方的指数移动平均，目的也相同——加权平均既保留了“陡峭”信号，又滤掉了单步噪声。超参数β是衰减率（通常取0.9），控制历史梯度平方的权重。跟动量法的$\mu$作用一样，却并不是同一个超参数。有的框架（比如pytorch）把它们叫做β1和β2加以区分。跟之前L2loss一样，这里也使用平方消除方向，不过为了使得参数更新量跟梯度保持一致，再用平方根数值变回之前的量级。

自适应学习率的威力

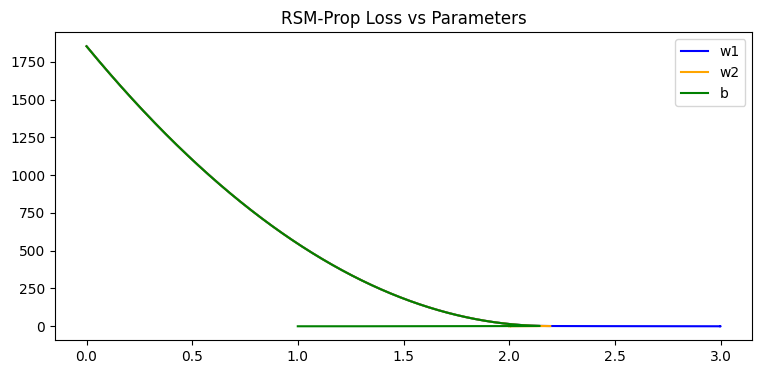
引入自适应学习率以后所有参数以相近”速度”收敛，只在最后阶段表现出区别。从图中可以看到，RMSProp的下降比较平滑，特别适用于噪音较多的数据。虽然在简单的数据上可能需要更多的训练次数，但在复杂的实际场景中，它具有更好的容错性、抗噪性和稳定性。 RMSprop

Adam: 集大成者

Adam (Adaptive Moment Estimation) 算法是目前最流行、最常用的优化算法之一。它的名字已经揭示了其本质：它结合了自适应学习率也就是RMSProp和动量法的思想。同时跟踪并计算了梯度的均值，即动量和非中心方差，即RMSProp中的梯度平方的指数移动平均。

具体来说，Adam的参数更新步骤如下：

计算梯度的一阶矩估计（动量）。
计算梯度的二阶矩估计（梯度平方的移动平均）。
使用这两个估计值来调整学习率。
更新参数。

@dataclass(frozen=True)
class AdamConfig(GDConfig):
    decay: float = 0.9      # 二阶矩衰减率β₂
    momentum: float = 0.85  # 一阶矩衰减率β₁
    eps: float = 1e-8       # 数值稳定常数

# 定义参数结构：参数+动量+自适应项
AdamP = namedtuple("AdamP", ["parameter", "velocity", "running_avg"])

def adam_i(p: P) -> AdamP:
    """初始化：零值动量和自适应项"""
    return AdamP(p, zeros(p), zeros(p))

def adam_d(adam_p: AdamP) -> P:
    """解包：提取原始参数"""
    return adam_p.parameter

def adam_u(adam_p: AdamP, g: Tensor, h: AdamConfig) -> AdamP:
    """Adam更新规则：
    1. 更新动量: v = β₁·v_old + (1-β₁)·g
    2. 更新自适应项: r = β₂·r_old + (1-β₂)·(g⊙g)
    3. 计算有效学习率: lr_eff = α / (√r + ε)
    4. 更新参数: θ = θ - lr_eff·v
    """
    v = smooth(h.momentum, adam_p.velocity, g)
    r = smooth(h.decay, adam_p.running_avg, tsqr(g))
    new_lr = tdiv(h.lr, tadd(tsqrt(r), h.eps))
    p = tsub(adam_p.parameter, tmul(new_lr, v))
    return AdamP(p, v, r)

# 构建Adam优化器
adam_gd = gradient_descent_builder(adam_i, adam_d, adam_u)

因为结合和RMSProp和动量法的思想，所以adam继承了双方的优点，在各种不同的问题和模型上都表现良好。可视化的结果看起来和RMSProp没什么区别，但是收敛速度更快，不过不如动量法快。

由于其诸多优点，还有其超参数默认值(β1=0.9, β2=0.999)适用大多数场景，Adam及其变体(AdamW, Nadam)已成为大多数深度学习任务的默认优化器。

总结

本文我们从最基础的批量梯度下降出发，踏上了一条优化算法的演进之路。

随机梯度下降（SGD）通过小批量更新，极大地提升了训练速度。
动量法（Momentum）通过引入惯性，帮助算法在正确的方向上加速，并抑制震荡。
RMSProp则通过自适应地调整每个参数的学习率，使得优化过程更加高效。
Adam作为集大成者，结合了动量和自适应学习率的优点，成为当今深度学习领域的“瑞士军刀”。

理解这些优化算法的原理和动机，对于我们诊断和调试神经网络的训练过程至关重要。

看完文章你肯定想自己运行代码尝试一下，跑代码时大概率会直接蹦出一堆 NaN——别慌,这不是你代码或者机器的问题，这个问题的出现实际上标志着我们的优化器工作得”太好了”—它们成功地将损失降到了数值微分方法无法处理的程度。这不是算法缺陷，而是数值方法的固有限制：随着训练，L2loss的值会逐渐逼近0，梯度计算会逐渐变成0.0/0.0，所以结果是Nan。可以暂时使用Jax的grad函数来代替我们的nabla实现来查看优化器的运行结果。如果你不想用JAX也不用担心，因为下一篇博客就讲自动微分。自动微分可能是深度学习学习中最重要也是最硬核部分，千万不要错过。